(備忘録)センター数学は東大京大対策になる byうすぴすさん
はじめに
この記事では、私が好んで見ていたYouTuberである、うすぴすさん(チャンネル)の動画について取り上げます。うすぴすさんは、現在はYouTube動画をすべて非公開にしてしまっているため、私自身が忘れないようにするための記録でもあります。記憶を掘り起こしながらの記載になりますことをお許しください。
彼はかつて動画で、センター数学(現在は大学入学共通テスト)の過去問を自学に用いる際の方法論を述べていました。ちなみにこのブログの著者は特に高校数学に長けている人間ではありませんし、工業高校卒でどちらかと言えば数学能力が低い(というか能力が高いところがひとつもない)人間なので、あらかじめご承知おきいただけますと幸いです。うすぴす氏が題材として取り上げていたのは、2018年度(平成30年度)センター試験の数学Ⅰ・Aの第一問になります。
私は、うすぴすさんのセンター数学タイムアタックの、圧倒的な思考速度や計算力も衝撃だったのですが、この記事で取り上げる「センター数学は二次試験対策になるよ」という趣旨の動画の方が好きだったので、記録したいと思いました:)
うすぴすさんについて
彼はセンター数学2019のⅠ・Aを初見でタイムアタックとして12分39秒で解いていた猛者で、その動画がバズっていました。記憶ではうすぴすさんが動画を非公開にする前には720万回再生されていた記憶があります。しかし、それもバズることを見越して(現役の時に周りに上下学年も含めそんなに速く解ける人間がいないことを知って)やった趣旨のことを後に述べていました。それから、他のチャンネルでもセンター試験タイムアタック動画が流行り始め、ある意味先駆者である彼は、それ自体と、それが誤魔化し(初見ではない)を含むものであると見抜けない、他チャンネル信者の視聴者に嫌気がさして、全動画を非公開としYouTubeから離れてしまったようです。
問題と向き合う時の基本的な考え方
さて、まず基本的な考え方ですが、彼が述べていたのは、センター試験は国の偉い人たちが1年間考えて作った問題なのだから、それにはそれ相応の意味があり、彼は現役時代にセンター数学を用いて自学していたそうです。問題を解くときの姿勢としては、出題者・作問者の意図、すなわち、どういうことを受験生に行わせたいのか、⓵どう解かせたいのかを考えること、そのために、⓶いきなり問題を頭から解き始めるのではなく全体を見渡し流れを読むこと、この二つのことを述べていました。加えて、センター試験は、⓷ひとつのことを受験生にやらせたいだけだとも述べていました。
そして、大学個別の二次試験は、センター数学の誘導を無くし結論をいきなり問うような形で出題されるため、センター数学の過去問の結論を先にもってきて問いを立て(後述します)解いてみると、センター数学は、東大京大をはじめとする難関大数学二次試験の対策になるだろうと述べていました。
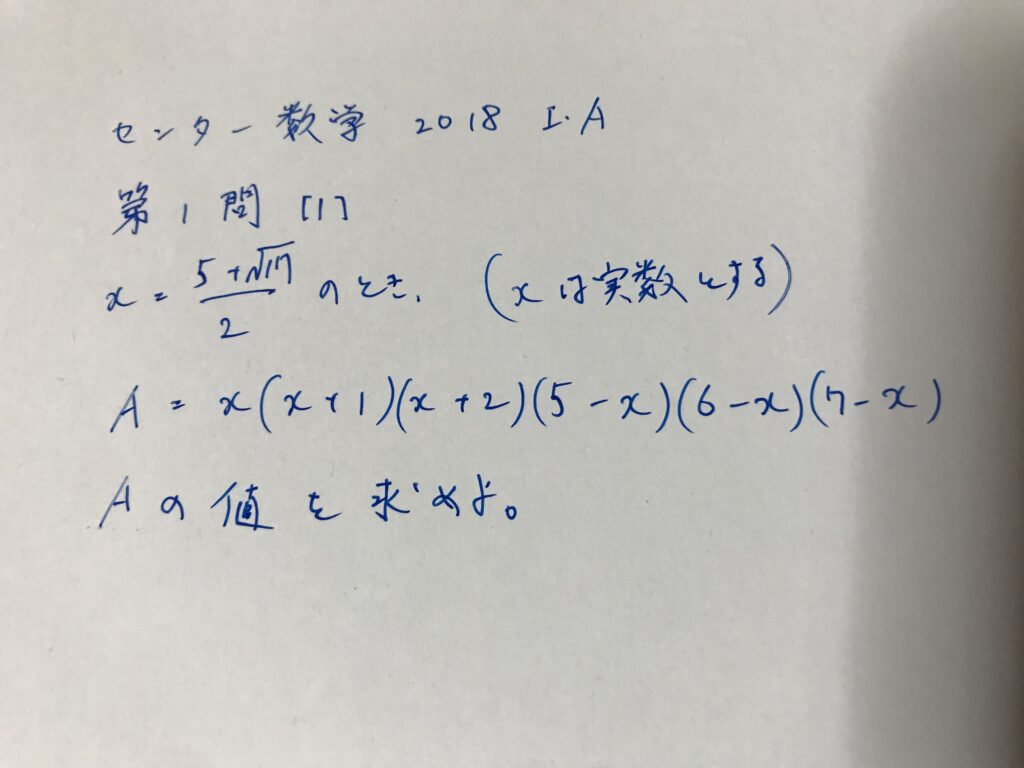
題材 : 2018年度センター数学Ⅰ・A 第一問
\(x \)を実数とし
$$ A = x(x+1)(x+2)(5-x)(6-x)(7-x) $$
とおく。整数\(n \)に対して
$$ (x + n )(n +5 - x) = x(5 - x) + n^2 +\text{ア}n $$
であり,したがって,\(X=x(5-x)\)とおくと,
$$ A = X(X + \text{イ})(X + \text{ウエ}) $$
と表せる。
\( x = \frac{(5+\sqrt{17})}{2} \) のとき,\( X = \text{オ}\) であり,\( A = 2^\text{カ}\) である。

センター数学は難関大の二次対策になる
さて、題材は2018年センター数学Ⅰ・Aの問題でした。これを頭から普通に解くと、
$$ (x+n)(n+5-x) $$
$$= nx+x(5-x)+n^2+5n-nx $$
$$= x(5-x)+n^2+5n $$
よって、アは5(あえて区別しやすいようLETEX表記にはしていません)
ここで,\( X= x(5-x) \)として,
\( n=1 \)とおくと,\((x+1)(6-x)=X+6 \)
よって、イは6
\( n=2 \)とおくと,\((x+2)(7-x)=X+14 \)
よって、ウエは14
であるから,
$$ A = x(x+1)(x+2)(5-x)(6-x)(7-x) $$
$$ = X(X+6)(X+14) $$
\( x = \frac{5+\sqrt{17}}{2} \) のとき,\( X = {\frac{5+\sqrt{17}}{2}}\times{(5-\frac{5+\sqrt{17}}{2})} \)
$$ ={\frac{5+\sqrt{17}}{2}}\times{\frac{5-\sqrt{17}}{2}} $$
$$ =\frac{5^2-(\sqrt{17})^2}{4} $$
$$ =\frac{25-17}{4} $$
$$ =2 $$
よって、オは2
このとき,\( A = {2}\times{(2+6)}\times{(2+14)}\)
$$ = {2}\times{8}\times{16} $$
$$ = {2}\times{2^3}\times{2^4} $$
$$ = 2^8 $$
よって、カは8
以上が、普通に頭から解いた時の流れになるかと思います。おそらく、予備校の解答でも上記のような流れになるのではないでしょうか。ただ、多くの数学が苦手な受験生(私も含む)は、上記の誘導の流れがなぜ成立するのか、悩んでいることでしょう。
全体の流れを俯瞰してみる
うすぴすさんの考え方、主張に沿って全体の流れを俯瞰してみます。
まず、この問題では、実数\(x\)があり、その\(x\)を代入した計算結果となる\(A\)があります。次に、整数\(n\)に対して、\(A\)を求める式を置き換えた式が明示され、整数\(x\)を含む\(X\)を設定しています。そして、\(X\)によって、\(A\)を求める式を簡略化し、最終的に\(A\)を求めています。よって、一呼吸おいて全体を見渡すと最終的に求めたいのは\(A\)だとわかります。出題者の意図をいつでも100%読み取れるとは限らないと、うすぴす氏も注意していましたが、おそらくこの出題では、展開式をなるべく簡略化したうえで具体値を代入し解を求めるという、計算の基本的操作を受験生に行わせたいのでしょう。
センター数学の問題の結論を先にもってくる(二次試験対策)
もちろん計算力に長けた人間ならば\(A\)に直接\(x\)を代入し、求められないことはない(それもなかなか化け物だと思うが)と、うすぴす氏も述べていた記憶があります。ただ、上記で述べたように出題者の意図を考えてみると、出来る限り式を簡略化し、その簡略化の過程が誘導になっていることを意識します。そして、難関大の二次試験ではその誘導がなく、\(x\)を提示して\(A\)をいきなり求めさせる問題が多いです。よって、\(A\)を、つまり、求めたい結論を先に持ってきて、
\(x=\frac{5+\sqrt{17}}{2}\)のとき、\(A= x(x+1)(x+2)(5-x)(6-x)(7-x)\)を求めよ。
とすることで、二次試験の対策となります。うすぴす氏の解説は以下の通りです。(記憶を掘り起こしながら記載しています。ご了承ください。)
まず、\(A = x(x+1)(x+2)(5-x)(6-x)(7-x)\)の右辺に注目します。すると、
\((5-x)\)を基準( \(+0\) )とするように見ると、左から\((x+1)\)、\((x+2)\)、\((5-x+0)\)、\((5-x+1)\)、\((5-x+2)\)となっていることが読み取れます。この各項に、さらに\(x\)を乗じたものが\(A\)です。
この問題で、なぜ整数\(n\)が導入され、なぜ\((x+n)(n+5-x)\)と設定され受験生を誘導に乗せているのかが、ここで繋がり、より深く理解できます。
すなわち、\(x\)以降の式をいきなり展開するのは大変であるので、 \((x+1)\)の共通項が現れる場合と、\((x+2)\)の共通項が現れる場合とを、分けて考えます。後に\(n\)に代入するのは当然\(1\)と\(2\)になります。整数\(n\)を導入することで一般化し、実は次数を落として考えることができ、そして\(X\)を設定し、最後に具体値を計算しているのです。
したがって、整数\(n\)を用いて表すと、
$$ (x+n)(n+5-x) $$
うすぴす氏もここで\((x+n)(n+5-x)\)を展開します。
$$ (x+n)(n+5-x) $$
$$= nx+x(5-x)+n^2+5n-nx $$
$$= x(5-x)+n^2+5n $$
これは、\(n\)の二次式とみることができ、一旦\(x(5-x)\)を\(X\)とおきます。これも、教科書レベルの計算の基本操作であることがわかります。「チャート式」や「一対一対応の演習」でも、基礎扱いだと思われます。
$$= X+n^2+5n $$
ここに\(n=1\)の場合と、\(n=2\)の場合とを、それぞれ代入して求めます。
\(n=1\)のとき、\(X+6\)
\(n=2\)のとき、\(X+14\)
さて、\(A\)を求める式に戻ると、\(A=x(x+1)(x+2)(5-x)(6-x)(7-x)\)
これは、うすぴすさんの説明にもどると、\(A=x(x+1)(x+2)(5-x+0)(5-x+1)(5-x+2)\)でした。
したがって、置き換えを行った\(X=x(5-x)\)で表すと、
$$ A=X(X+6)(X+14) $$
これは、数学が苦手な受験生向けに一応記載しますが、
\(x(5-x+0)\)すなわち、\(n=0\)の場合が、\(X\)、
\((x+1)(5-x+1)\)すなわち、\(n=1\)の場合が、\(X+6\)、
\((x+2)(5-x+2)\)すなわち、\(n=2\)の場合が、\(X+14\)と、
当初の式を簡単にするために、整数\(n\)を用いて、\(X\)を置いたのだから自明です。
つづいて、\(X=x(5-x)\)に、一番最初に設定されている、\(x=\frac{5+\sqrt{17}}{2}\)を代入します。
$$ X = {\frac{5+\sqrt{17}}{2}}\times{(5-\frac{5+\sqrt{17}}{2})} $$
ここで、うすぴす氏は、受験テクニック的な話になると、\(x=\frac{5+\sqrt{17}}{2}\)のようなものが登場したときは、大体\(\pm\)で掛けさせる(和と差の積に終着させる)ことが多いと述べていました。私が感動したのは、上記の式が平均になっていると述べていたところでした。
つづきは、
$$ ={\frac{5+\sqrt{17}}{2}}\times{\frac{5-\sqrt{17}}{2}} $$
$$ =\frac{5^2-(\sqrt{17})^2}{4} $$
$$ =\frac{25-17}{4} $$
$$ =2 $$
\(X\)が求まったので、最後に\(A\)を求める簡略化した式に代入し、
$$ A=X(X+6)(X+14) $$
$$ ={2}\times{8}\times{16} $$
$$ = {2}\times{2^3}\times{2^4} $$
$$ = 2^8 $$
ここまでがうすぴす氏の解説の流れになります。記憶を掘り起こしているため、言い回しが異なる部分があるかも知れませんが、流れは踏襲しているものと思います。
上記のように結論を先にもっていき、誘導無しで解くことにしても、センター試験の誘導のように解を導けることがよく理解できるかと思います。私はうすぴす氏の解説を最初に見たときに「センター試験、奥深ぇ」と思いました。そりゃそうですよね。うすぴす氏が述べるように、国の偉い人たちが1年掛けて作問するのだから、これが二次試験対策になるのも頷けます。
所々流れがわかり辛いところがあったら申し訳ございません。ここまで駄文をお読みいただき、ありがとうございました。私ももういい歳なのですが、貯金ができたらまた大学受験に挑戦しようと思います。
ではまた。